یک مثال GAMS

این مساله فقط برای نشان دادن این است که چگونه GAMS به شما امکان می‌دهد به روشی طبیعی مدل‌سازی کنید. GAMS می تواند مشکلات بسیار بزرگتر و بسیار پیچیده را حل کند. فقط تعدادی از ویژگی های اساسی GAMS را می توان در اینجا برجسته کرد.

مدل ریاضی
در اینجا یک توصیف جبری استاندارد از مساله ارائه شده است، که به حداقل رساندن هزینه حمل کالا از ۲ کارخانه به ۳ بازار، مشروط به محدودیت های عرضه و تقاضا است.

اندیس ها:

مدل GAMS
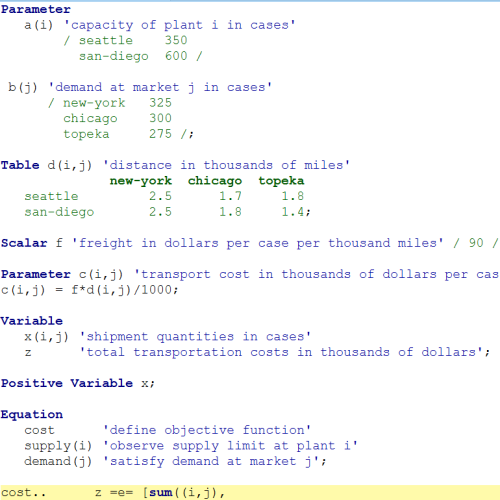
همان مدل در GAMS مدل سازی شده است. استفاده از توصیفات جبری مختصر، مدل را بسیار فشرده و دارای ساختار منطقی می کند. اسناد داخلی، مانند توضیح پارامترها و واحدهای اندازه گیری، خواندن مدل را آسان می کند.

Sets   
       i   canning plants   / Seattle, San-Diego /
       j   markets          / New-York, Chicago, Topeka / ;
Parameters
       a(i)  capacity of plant i in cases
         /    Seattle     350
              San-Diego   600  /
       b(j)  demand at market j in cases
         /    New-York    325
              Chicago     300
              Topeka      275  / ;
Table  d(i,j)  distance in thousands of miles
                  New-York       Chicago      Topeka
    Seattle          2.5           1.7          1.8
    San-Diego        2.5           1.8          1.4  ;
Scalar f  freight in dollars per case per thousand miles  /90/ ;
Parameter
       c(i,j)  transport cost in thousands of dollars per case ;
c(i,j) = f * d(i,j) / 1000 ;
Variables
     x(i,j)  shipment quantities in cases
     z       total transportation costs in thousands of dollars ;
Positive variables x ;
Equations
     cost        define objective function
     supply(i)   observe supply limit at plant i
     demand(j)   satisfy demand at market j ;
cost ..        z  =e=  sum((i,j), c(i,j)*x(i,j)) ;
supply(i) ..   sum(j, x(i,j))  =l=  a(i) ;
demand(j) ..   sum(i, x(i,j))  =g=  b(j) ;
Model transport /all/ ;
Solve transport using LP minimizing z ;