آموزش GAMS – قسمت هشتم: تعریف معادلات (Equations)

معادلات (Equations) چیست؟

در GAMS، معادلات روابط ریاضی هستند که تابع هدف (مثل کمینه کردن هزینه) و محدودیت‌های مدل (مثل ظرفیت یا تقاضا) را مشخص می‌کنند. معادلات به GAMS می‌گویند که چه چیزی را باید بهینه کند و چه شرایطی را باید رعایت کند.

انواع معادلات

1. تابع هدف (Objective Function):
   • هدفی که مدل دنبال می‌کند، مثل کمینه کردن هزینه یا بیشینه کردن سود.
   • مثال: کمینه کردن هزینه حمل کالا.
2. محدودیت‌ها (Constraints):
   • شرایطی که مدل باید رعایت کند، مثل تأمین تقاضا یا محدودیت ظرفیت.
   • مثال: هر شهر باید حداقل مقدار مشخصی کالا دریافت کند.
3. انواع رابطه:
   • =e= (مساوی): برای تابع هدف یا روابط دقیق.
   • =g= (بزرگ‌تر یا مساوی): برای حداقل‌ها (مثل تقاضا).
   • =l= (کوچک‌تر یا مساوی): برای حداکثرها (مثل ظرفیت).

نحوه تعریف معادلات در GAMS

معادلات با کلمه کلیدی Equations تعریف می‌شوند و سپس با استفاده از متغیرها و پارامترها نوشته می‌شوند. ساختار کلی به این شکل است:

Equations
  name(index) "توضیح";
name(index).. expression =e/=g/=l= value;

• name: نام معادله (مثل Cost یا Demand).
• index: مجموعه‌ای که معادله به آن وابسته است (اختیاری).
• “توضیح”: توضیح برای خوانایی.
• expression: رابطه ریاضی (مثل جمع متغیرها).
• =e/=g/=l: نوع رابطه (مساوی، بزرگ‌تر یا مساوی، کوچک‌تر یا مساوی).

مثال ساده: معادلات برای حمل‌ونقل

فرض کنید می‌خواهید هزینه حمل کالا از یک انبار به سه شهر را کم کنید. معادلات شامل تابع هدف (کمینه کردن هزینه) و محدودیت (تأمین تقاضا) هستند:

Sets
  i "شهرهای مقصد" /Tehran, Shiraz, Isfahan/;
Parameters
  c(i) "هزینه حمل" /Tehran 50, Shiraz 100, Isfahan 80/
  d(i) "تقاضا" /Tehran 200, Shiraz 300, Isfahan 250/;
Variables
  x(i) "مقدار حمل به هر شهر"
  z "هزینه کل";
Positive Variable x;
Equations
  Cost "هزینه کل"
  Demand(i) "تقاضای هر شهر";
Cost.. z =e= sum(i, c(i)*x(i));
Demand(i).. x(i) =g= d(i);
Model Transport /all/;
Solve Transport using LP minimizing z;
Display x.l, z.l;

• معادله Cost:
  • z =e= sum(i, c(i)*x(i)): هزینه کل (z) برابر است با مجموع هزینه حمل (c(i)) ضرب در مقدار حمل (x(i)).
• معادله Demand:
  • x(i) =g= d(i): مقدار حمل به هر شهر (x(i)) باید حداقل برابر تقاضا (d(i)) باشد.
• مدل و حل:
  • Model Transport /all/: تمام معادلات را شامل می‌شود.
  • Solve Transport using LP minimizing z: مدل را به‌عنوان برنامه‌ریزی خطی حل می‌کند و هزینه کل (z) را کمینه می‌کند.
• نمایش:
  • Display x.l, z.l: مقادیر بهینه مقدار حمل (x) و هزینه کل (z) را نشان می‌دهد.

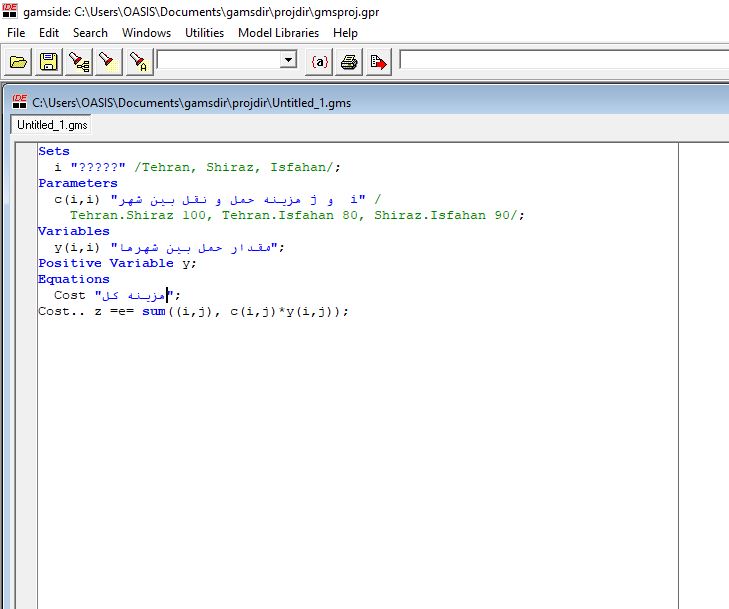
معادلات چندبعدی

برای مسائل پیچیده‌تر، می‌توانید معادلات را روی مجموعه‌های چندبعدی تعریف کنید. مثلاً برای حمل بین جفت شهرها:

Sets
  i "شهرها" /Tehran, Shiraz, Isfahan/;
Parameters
  c(i,i) "هزینه حمل بین شهرها" /
    Tehran.Shiraz 100, Tehran.Isfahan 80, Shiraz.Isfahan 90/;
Variables
  y(i,i) "مقدار حمل بین شهرها";
Positive Variable y;
Equations
  Cost "هزینه کل";
Cost.. z =e= sum((i,j), c(i,j)*y(i,j));

• sum((i,j), c(i,j)*y(i,j)): هزینه کل برای تمام جفت شهرها محاسبه می‌شود.

نکات مهم در تعریف معادلات

• خوانایی: از نام‌های معنادار (مثل Cost یا Demand) و توضیحات استفاده کنید.
• وابستگی به مجموعه‌ها: معادلات معمولاً روی مجموعه‌ها (Sets) تعریف می‌شوند.
• دقت در روابط: از =e=، =g=، یا =l= درست استفاده کنید (مثلاً =g= برای حداقل تقاضا).
• خطاها: اگر معادله نادرست باشد (مثلاً متغیر تعریف‌نشده)، GAMS خطا می‌دهد. فایل .lst را بررسی کنید.

مثال عملی: مسئله حمل‌ونقل

برای کمینه کردن هزینه حمل کالا:

• مجموعه‌ها: شهرها (i).
• پارامترها: هزینه (c) و تقاضا (d).
• متغیرها: مقدار حمل (x) و هزینه کل (z).
• معادلات: تابع هدف (Cost) و محدودیت تقاضا (Demand).
• خروجی: GAMS مقادیر بهینه حمل (مثل ۲۰۰ واحد به تهران) و هزینه کل را نشان می‌دهد.

ویدئوی آموزشی (۲ دقیقه)

در ویدئوی این قسمت:

• مفهوم معادلات (تابع هدف و محدودیت‌ها) را با نمودار ساده توضیح می‌دهیم.
• کد نمونه بالا را در GAMS Studio می‌نویسیم و اجرا می‌کنیم.
• خروجی Display x.l, z.l را در پنجره Log نمایش می‌دهیم.

لینک ویدئو: [لینک آپارات یا یوتیوب، پس از آپلود اضافه کنید]

نکات کلیدی

• معادلات: تابع هدف و محدودیت‌ها را تعریف می‌کنند.
• انواع: تابع هدف (مثل کمینه کردن هزینه) و محدودیت‌ها (مثل تقاضا).
• تعریف: با Equations و روابط =e=، =g=، یا =l=.
• کاربرد: قلب مدل‌سازی برای رسیدن به جواب بهینه.

گام بعدی

در قسمت بعدی، با ساختار یک کد ساده در GAMS آشنا می‌شوید و یک مدل کامل را از ابتدا می‌نویسید. فایل‌های نمونه و ویدئوهای این دوره را از سایت بهینه‌یار دانلود کنید!

کلمات کلیدی: آموزش GAMS، تعریف معادلات در GAMS، مدل‌سازی بهینه‌سازی، GAMS برای مبتدیان، بهینه‌یار